データ分析っぽいことをする場合、最初に必要となるのが要約統計量(基本統計量)です。
Pythonでは、pandas 、 numpy 、statistics といったライブラリで簡単に計算が可能なので、それぞれのサンプルソースを提示して解説したいと思います。
要約統計量(基本統計量)とは
データの分布状態や、特徴を表すために用いられる数値で、次のものがあります。
| 平均値 | 全データを足して個数で割った値 |
|---|---|
| 中央値 | 全データを大きさ順に並べた時に真ん中にある値 (四分位点=50%のこと) |
| 最頻値 | 全データの中で最も多く登場する値 |
| 分散 | 全データのバラつき具合 |
| 標準偏差 | 全データのバラつき具合(分散の平方根) |
| 最大値 | 全データの中で最大の値 |
| 最小値 | 全データの中で最小さい値 |
| 合計値 | 全てのデータの合計値 |
| 歪度 | 分布における左右の非対称さの度合い |
| 尖度 | 分布の山の尖がり具合 |
| 四分位点(パーセンタイル) | 全データを大きさ順に並べた時、25%、50%、75% に位置する値(中央値は50%の値を意味する) |
pandasで要約統計量 を計算するには
pandasでは、1つのメソッドで主要な統計量を一括で取得する方法と、個々の統計量 を指定して取得する方法の2通りがあります。
統計量を一括して取得する
describe メソッドにより主要な統計量 を表示することが出来ます。
import numpy as np
import pandas as pd
#正規分布の乱数を使ってテストデータを作成(平均値:loc、標準偏差:scale、データ数:size)
data1 = np.random.normal(loc=50, scale=25, size=100)
data2 = np.random.normal(loc=20, scale=10, size=100)
data3 = np.random.normal(loc=10, scale=5, size=100)
df = pd.DataFrame({'col1':data1,'col2':data2,'col3':data3})
#統計量の表示
df.describe()
結果はDataFrameで次のように返されます。
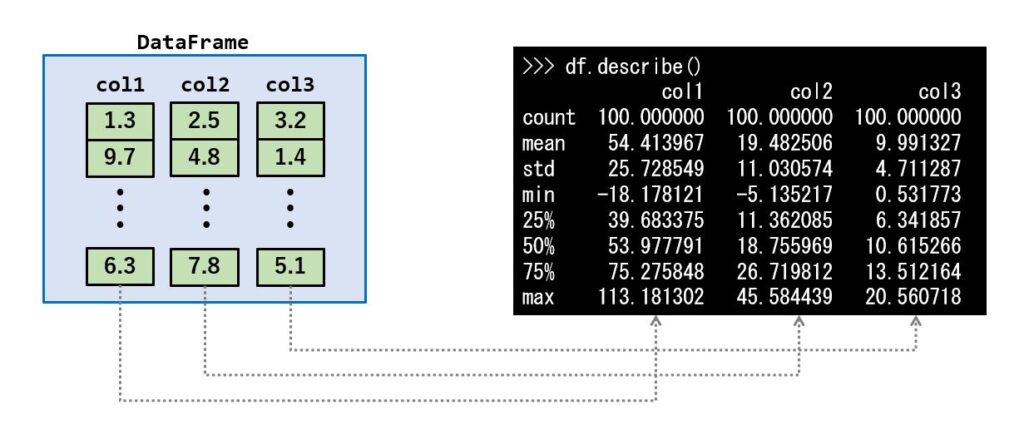
個々の統計量 を取得する
統計量 を取得するためのメソッドとして、以下のものが用意されています。
| 平均値 | mean() |
|---|---|
| 中央値 | median() |
| 最頻値 | mode() |
| 分散 | var(ddof=1) ddof=0:標本分散(与えられたデータの分散) ddof=1:不偏分散(与えられたデータから推定した母集団の分散) ※ddof 省略時は標本分散(ddof=0) |
| 標準偏差 | df.std(ddof=1) ddof=0:標本分散(与えられたデータの分散) ddof=1:不偏分散(与えられたデータから推定した母集団の分散) ※ddof 省略時は標本分散(ddof=0) |
| 最大値 | max() |
| 最小値 | min() |
| 合計値 | sum() |
| 歪度 | skew() |
| 尖度 | kurt() |
| 四分位点(パーセンタイル) | quantile(q=[0.25,0.5,0.75]) q=取得したい四分位点を指定 0.6 や 0.8 などの任意の値も指定できる |
下記は実際のサンプルソースです。
import numpy as np
import pandas as pd
#正規分布の乱数を使ってテストデータを作成(平均値:loc、標準偏差:scale、データ数:size)
data1 = np.random.normal(loc=50, scale=25, size=100)
data2 = np.random.normal(loc=20, scale=10, size=100)
data3 = np.random.normal(loc=10, scale=5, size=100)
df = pd.DataFrame({'col1':data1,'col2':data2,'col3':data3})
#個々の統計量の取得
print('平均',df.mean())
print('中央値',df.median())
print('合計',df.sum())
print('分散',df.var(ddof=1))
print('標準偏差',df.std(ddof=1))
print('最大',df.max())
print('最小',df.min())
print('歪度',df.skew())
print('尖度',df.kurt())
print('四分位',df.quantile(q=[0.25,0.75]))
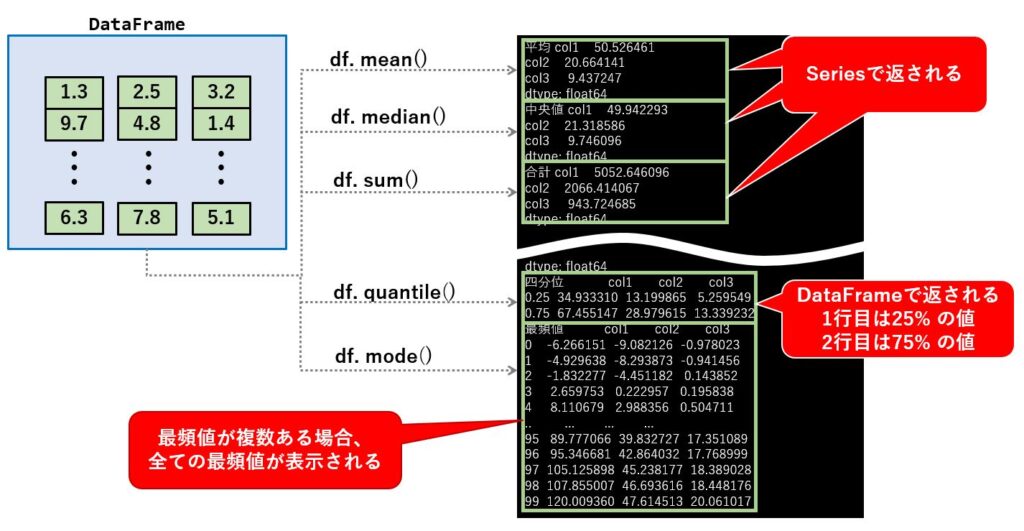
print('最頻値',df.mode())
実行結果は以下の様になります。
個々の統計量は Series で返されますが、 quantile と mode はDataFrame で返されます。
df (2次元)ではなく Series(1次元) に対して統計量を求めても、戻り値は Series で返されます。
numpyで要約統計量を計算するには
mumpy には 主要な統計量を一括して取得するメソッドが用意されていないため、それぞれについて統計量を取得しなければなりません。
また、歪度、尖度、最頻値を求めるメソッドは用意されていないため、scipy の stats モジュールを使う必要があります。
import numpy as np
from scipy import statsnumpy には次のメソッドが用意されています。ほぼ pandas と同じですが、引数にデータを渡すところが異なります。
| 平均値 | np.mean(data) |
|---|---|
| 中央値 | np.median(data) |
| 最頻値 | stats.mode(data) |
| 分散 | np. var(data,ddof=1) ddof=0:標本分散(与えられたデータの分散) ddof=1:不偏分散(与えられたデータから推定した母集団の分散) ※ddof 省略時は標本分散(ddof=0) |
| 標準偏差 | df.std(data,ddof=1) ddof=0:標本分散(与えられたデータの分散) ddof=1:不偏分散(与えられたデータから推定した母集団の分散) ※ddof 省略時は標本分散(ddof=0) |
| 最大値 | np. max(data) |
| 最小値 | np. min(data) |
| 合計値 | np. sum(data) |
| 歪度 | stats. skew() |
| 尖度 | stats. kurtosis() |
| 四分位点(パーセンタイル) | np.percentile(data, 25) #25%パーセンタイル np.percentile(data, 75) #75%パーセンタイル |
下記は具体的なサンプルソースですが、pandas でテスト用の2次元データを作っているため、pandas をimport しています。
import numpy as np
import pandas as pd
from scipy import stats
#正規分布の乱数を使ってテストデータを作成(平均値:loc、標準偏差:scale、データ数:size)
data1 = np.random.normal(loc=50, scale=25, size=100)
data2 = np.random.normal(loc=20, scale=10, size=100)
data3 = np.random.normal(loc=10, scale=5, size=100)
df = pd.DataFrame({'col1':data1,'col2':data2,'col3':data3})
data = df.values
print('平均値:', np.mean(data))
print('中央値:', np.median(data))
print('合計:', np.sum(data))
print('分散',np.var(data,ddof=1))
print('標準偏差',np.std(data,ddof=1))
print('最大',np.max(data))
print('最小',np.min(data))
print('歪度',stats.skew(data))
print('尖度',stats.kurtosis(data))
print('四分位点(25%):', np.percentile(data, 25))
print('四分位点(50%):', np.percentile(data, 50))
print('四分位点(75%):', np.percentile(data, 75))
print('最頻値:', stats.mode(data))実行結果は以下の様になります。
pandas と異なり、歪度、尖度、最頻値 以外は列に関係なく全ての値を使って統計量が計算されます。
歪度、尖度は ndarray で値が返され、最頻値は ModeResult という型で値が返されます。

ModeResultには mode と count のプロパティがあり、 mode で 列ごとの最頻値が、count で最頻値の個数が取得できます。
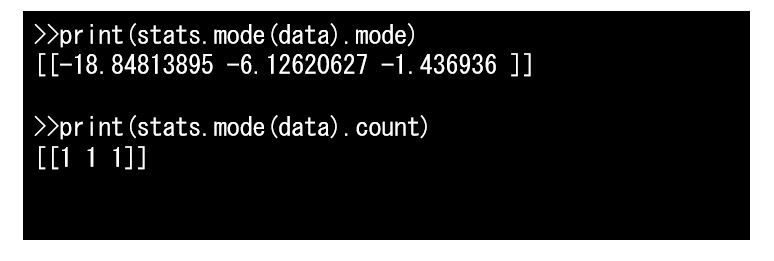
statistics で要約統計量を計算するには
statistics というライブラリを import することで、統計情報を取得することも出来ます。
import statistics尚、こちらは一次元データのみに対応しているので、2次元以上のデータを入れるとエラーになります。
使い方は numpy と同じく 各メソッドの引数にデータえることで計算が可能ですが、最大、最小、合計、歪度、尖度、四分位点のメソッドは用意されていません。
| 平均値 | statistics.mean(data) |
|---|---|
| 中央値 | statistics.median(data) |
| 最頻値 | statistics.mode(data) |
| 分散 | 標本分散:statistics.variance(data) 不偏分散:statistics.pvariance(data) |
| 標準偏差 | 標本分散:statistics.stdev(data) 不偏分散:statistics.pstdev(data) |
| 最大値 | 用意されていないので、 python 標準の max(data) で代用 |
| 最小値 | 用意されていないので、 python 標準の min(data) で代用 |
| 合計値 | 用意されていないので、python 標準の sum(data) で代用 |
| 歪度 | 用意されていない |
| 尖度 | 用意されていない |
| 四分位点(パーセンタイル) | 用意されていない |
下記はサンプルソースです。
#テストデータを作成
import numpy as np
data = np.random.normal(loc=50, scale=25, size=100)
#要約統計量を取得
import statistics
print('平均値:', statistics.mean(data))
print('中央値:', statistics.median(data))
print('合計:', sum(data))
print('母分散',statistics.pvariance(data))
print('分散',statistics.variance(data))
print('母標準偏差',statistics.pstdev(data))
print('標準偏差',statistics.stdev(data))
print('最大',max(data))
print('最小',min(data))
print('最頻値:', statistics.mode(data))実行結果は次の様になりました。
平均値: 47.26833908244574
中央値: 48.166835711938205
合計: 4726.833908244576
母分散 532.6284044944802
分散 538.0084893883638
母標準偏差 23.078743564034852
標準偏差 23.19501001052519
最大 109.65097660255452
最小 -3.24616100773617
最頻値: 61.715723790847946
まとめ
今回はpandas と numpy のそれぞれについて、要約統計量 (基本統計量)の求め方について、図とサンプルソースを交えて解説致しました。
データを分析する際、そのデータがどういう分布なのか、どいういう性質を持つのかを知ることは非常に大切です。
このような統計量が簡単に取得できるのは Python の強みです。
今回の記事が皆さんのプログラミングの一助になれば幸いです。








コメント