時々ですが、仕事の関係で２つの文字列がどれくらい一致するかを数値で表したくなることがあります。
この記事に辿り着いたあなたは、きっと私と同じ思いをされていることでしょう。
文字列の類似度といえば、レーベルシュタイン距離や、ジャロ・ウィンクラー距離などが有名ですが、N-gramとコサイン類似度を使う方法も良く登場します。
「文字列 類似度」で検索すると、「川村インターナショナル」という企業のブログのこの記事に詳しく書かれていたので、これをC#で実装してみたのが今回の記事になります。
記事では、「文の類似度」として紹介されていますが、アプリケーションから入力された文字列の名寄せに使えそうなので、興味のある方はご一読ください。
N-gramとは
簡単にN-gram について紹介しておきます。
N-gram とは、文字列を左から順に１文字づつスライドさせながら、Ｎ個を取り出していく（＝分解していく）方法です。
日本語の分解方法としてはMecabやJanomeなどの形態素解析が主に使われますが、これには辞書が必要です。
Ｎ-gramは辞書を使うことなく機械的に分解していくことができるので、言語の種類を問わず利用できるというメリットがあります。
N-gramのNは取り出す文字数を表しており、１文字づつ取り出す場合はユニグラム、２文字づつ取り出す場合はバイグラム、３文字づつ取り出す場合はトライグラム（又はトリグラム）という別名でも呼ばれています。
コサイン類似度
コサイン類似度は、ベクトル同士の向きに着目して類似性を判断する方法で、ベクトル同士の角度が小さいほど、両者は似ていると判断します。
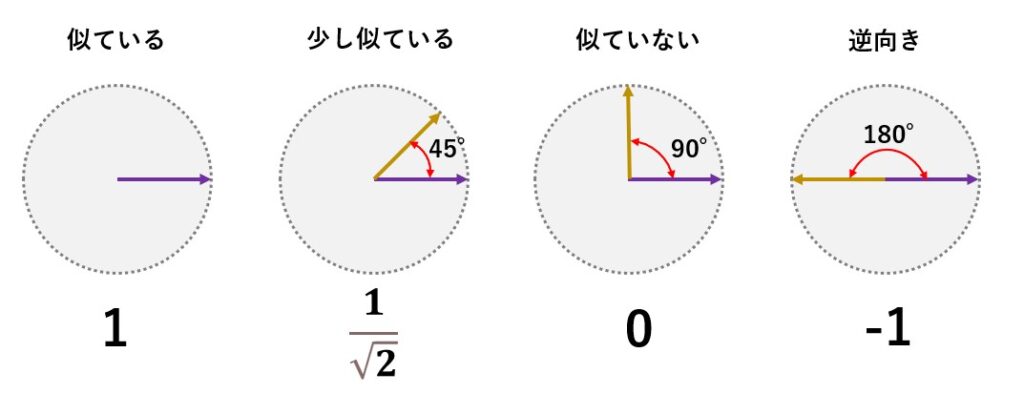
計算方法は以下の計算式を用います。
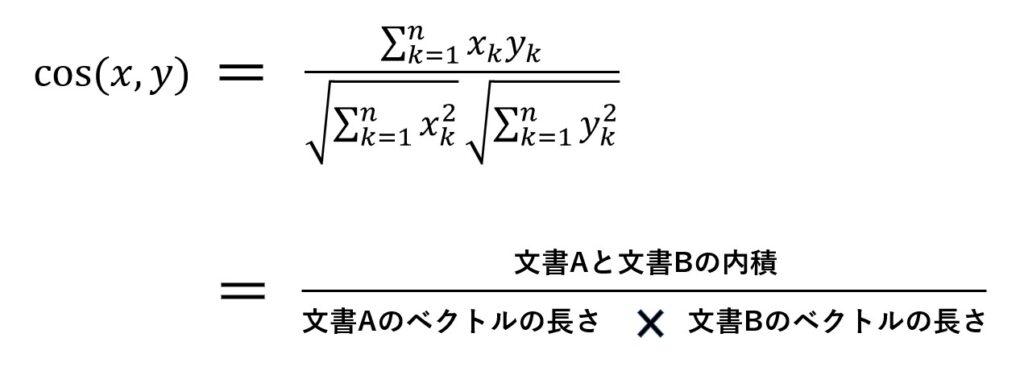
文書Aと文書Bをそれぞれベクトル化し、その結果を上記の式に代入することで、コサイン類似度が求まります。
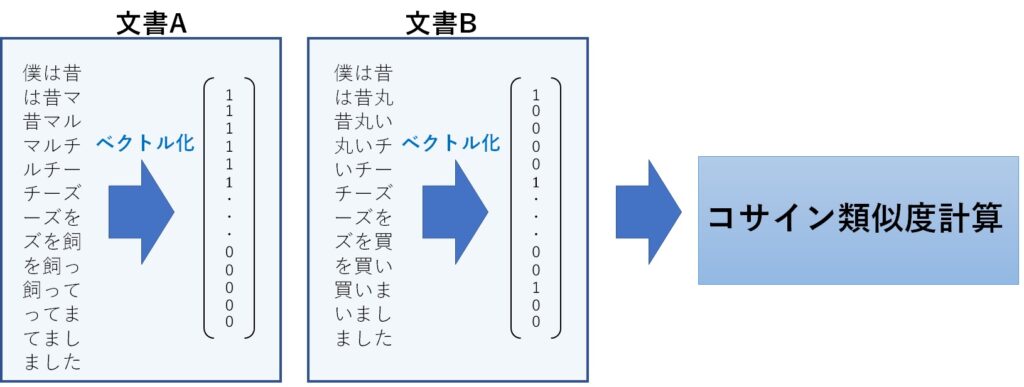
文書Aと文書Bのベクトル化は、それぞれの文書から求めたN-gramの結果を重複部分を取り除いて１つに結合します。
そして、その結合結果に対して、文書Aと文書Bのそれぞれの中身を突き合わせ、あれば１，なければ０としてベクトルを作成します。
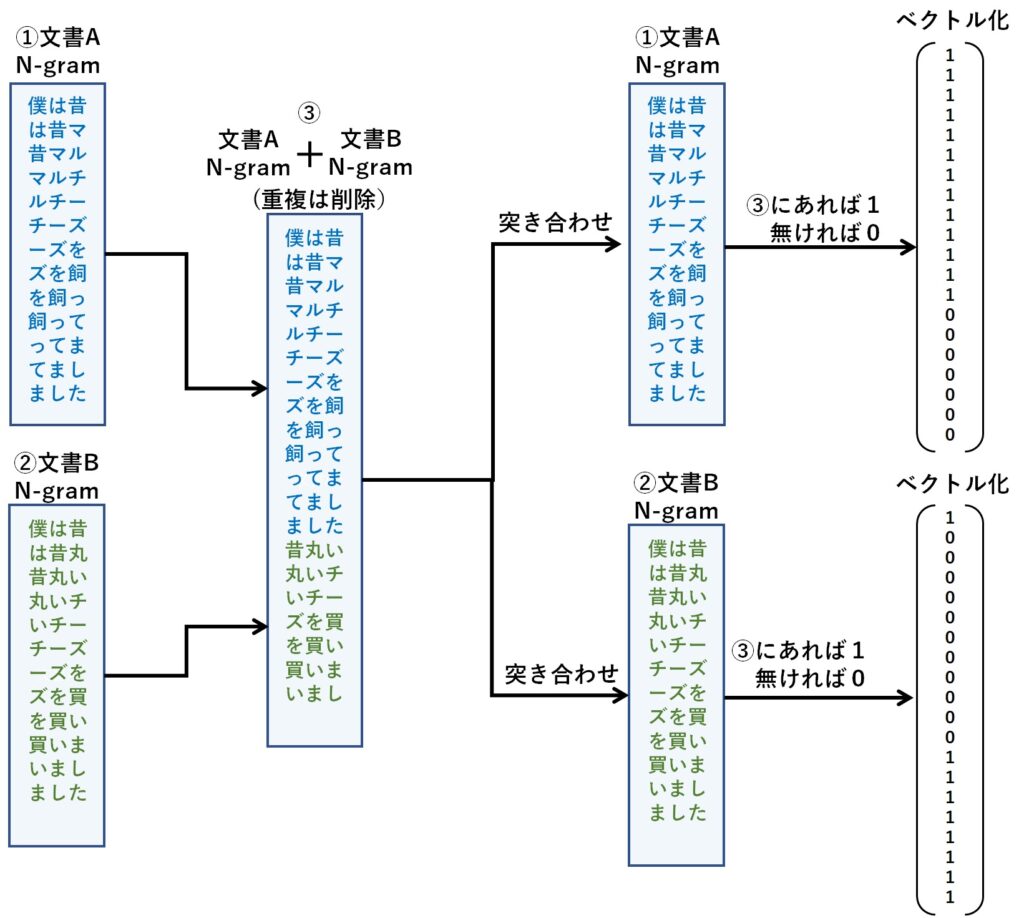
N-gram とコサイン類似度による類似度計算
詳しくは「川村インターナショナル」のこの記事 に大変分かりやすく解説されていますので、私の記事では簡単に概要のみ紹介します。
文書をベクトル化する際、単純にユニグラム、バイグラム、トライグラムのいずれか１種類で分割してコサイン類似度を求めてもよいのですが、例えば使われている文字の種類が少ない場合、ユニグラムだと類似度が高く、トライグラムだと類似度が低いという正反対の結果になるかもしれません。
そこで、以下の工夫を行うことで、より安定した類似度が計算できるようにしています。
ユニグラム、バイグラム、トライグラムを求め、合算してベクトル化する
文書A,文書Bの両方に対して、unigram、bigram、trigram を求め、それらを合算（結合）した結果からベクトルを求めます。
１つの文書で重複部分が有る場合、連番を付けて個別に扱う。
１つの文書の中に重複部分が有る場合、一般的には重複削除していましたが、今回は削除せず、連番を付けて個別のものとして取り扱います。
ソースコード
以上の内容のC#でコード化した結果を紹介しておきます。
関数化していますので、コピー＆ペーストしてお使いください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
public double NgramCosineSimilarity(string str1, string str2) { var str1_tkn = ngram(str1); var str2_tkn = ngram(str2); var join = new HashSet<string>(str1_tkn); str2_tkn.Select(i => join.Add(i)).ToArray(); var str1_vec = join.Select(i => str1_tkn.Contains(i) ? 1 : 0).ToArray(); var str2_vec = join.Select(i => str2_tkn.Contains(i) ? 1 : 0).ToArray(); return CalcCosineSimilarity(str1_vec, str2_vec); List<string> ngram(string p_str) { var l_dic = new Dictionary<string, int>(); if (p_str != "") { for (int n = 1; n <= 3; n++) { for (int i = 0; i < p_str.Length - (n - 1); i++) { var l_key = p_str.Substring(i, n); if (!l_dic.ContainsKey(l_key)) { l_dic.Add(l_key, 0); } l_dic[l_key]++; } } } List<string> words = new List<string>(); foreach (var kvp in l_dic) { words.AddRange(Enumerable.Range(0, kvp.Value).Select(i => kvp.Key + (i + 1).ToString()).ToList()); } return words; } } |
下記はこの関数を使った具体例になります。
|
1 2 3 4 5 6 |
//使い方 var res = NgramCosineSimilarity("僕は昔マルチーズを飼ってました", "僕は昔丸いチーズを買いました"); //結果(resの中身) 0.51887452166277082 |
まとめ
今回は、文字列の類似度をN-gramとコサイン類似度で求める方法について紹介しました。
一般的にはN-gram を１回通して、重複を削除してからベクトル化する方法が多いですが、今回はユニグラム、バイグラム、トライグラムを求めて、重複を削除せずベクトル化するという方法を用いています。
詳しくは「川村インターナショナル」のこの記事に委ねるとして、私の記事ではC#でこれを実現し、関数化しておいたので、もし利用する用途があれば、コピペしてお使い下さい。
今回の記事が皆さんのプログラミングの参考になれば幸いです。
コメント