「加重平均」というキーワードで調べた時、よく中身を読まないと中身が理解できない記事が多かったので、今回は図を入れて丁寧に解説致します。
仕事で「加重平均で計算して!」と言われて、「どうだったっけ~?」という方に向けた記事になります。
加重平均とは
加重平均とは、複数の集団からそれぞれに平均値が出されていて、その平均値を使って全体の平均値を出したい場合、元の集団の規模を加味して平均値を計算する方法です。
例えば、とある会社の平均年齢を考えてみましょう。
その会社には5人の従業員がいて、下記のような年齢だったとします。

この場合の平均は、単純に年齢を合計して人数で割ればよいので、次のようになります。
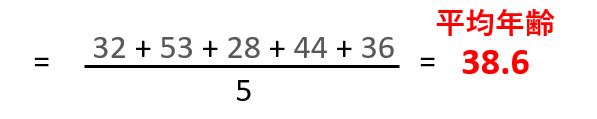
では、次のようなケースを考えてみましょう。
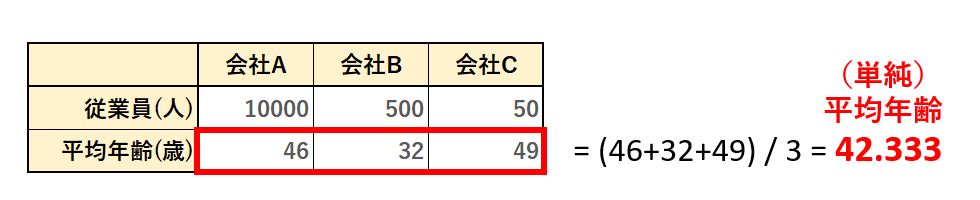
会社A、会社B、会社C があって、それぞれの会社で既に平均年齢が計算されていたとします。
では、この会社A、会社B、会社Cの平均年齢から、全体の平均年齢を求める場合はどうすればよいでしょう?
単純に考えるなら、それぞれの平均年齢を合計して、会社の数で割れば計算できます。
でも、ちょっと待ってください。
確かにこの方法でも平均は求まりますが、従業員数が全く違うので、会社Cの年齢が高齢側に偏っていたらどうでしょう?
少人数の平均値が、全体の平均値に大きく影響してしまいますよね。
このような問題を回避するため、その背景にある規模の違い(平均値の元となる集団の大きさ)を加味して平均を出す方法が「加重平均」です。
加重平均の求め方(方法1)
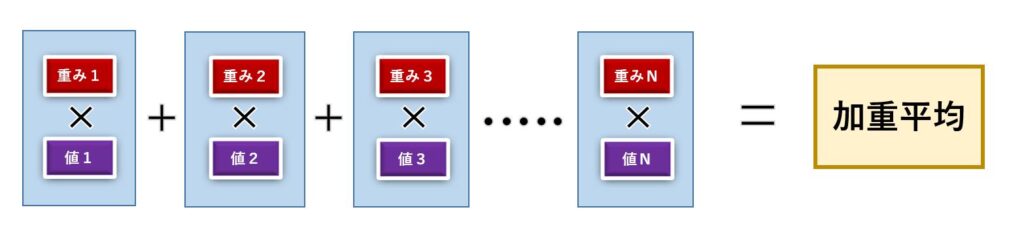
加重平均は、背景にある規模の違いを、「重み=加重」という値で表し、それぞれの「値」に「重み」を掛けて、最後に合計することで求めることが出来ます。
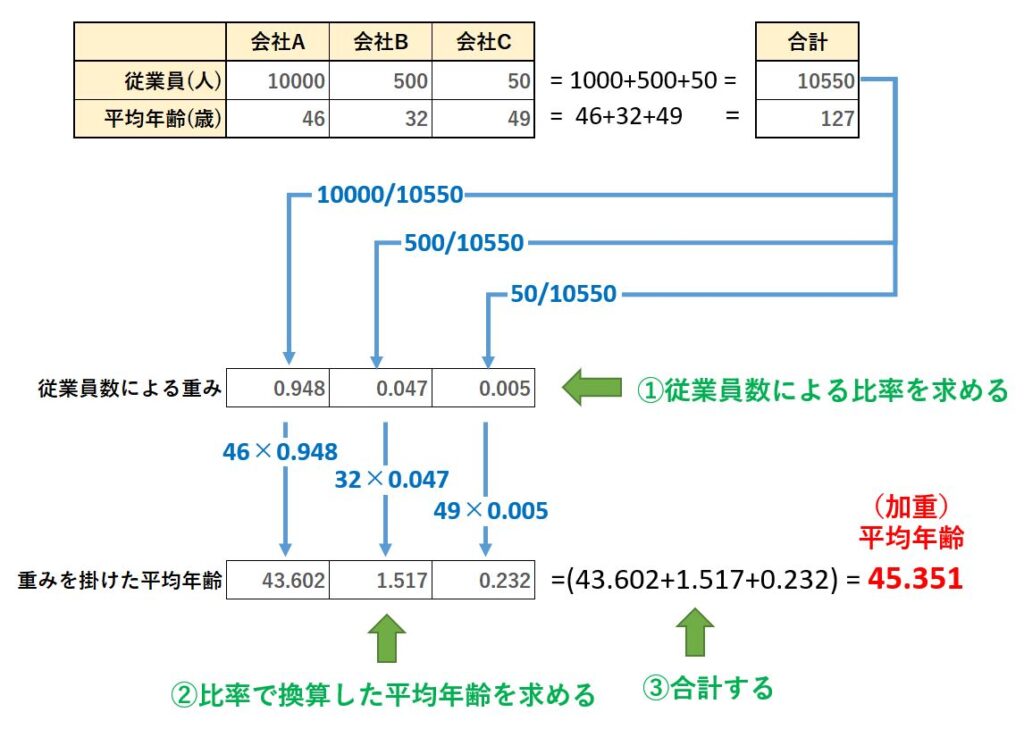
今回のケースでは、規模の大小は従業員となりますから、まず会社ごとの「比率=重み」を計算します。
具体的には、各会社の従業員の合計を出して、各会社の従業員数で割ります(①従業員数による比率を求める)。
これが「重み」となるため、この「重み」を、各会社の年齢に掛け算します(②
比率で換算した平均年齢を求める)。
ここまで出来たら、後は重みづけされた平均年齢を合計するだけです(③合計する)
こうすることによって、規模を考慮した平均「加重平均」が求まります。
加重平均の求め方(方法2)
加重平均の求め方については、もう1つあります。
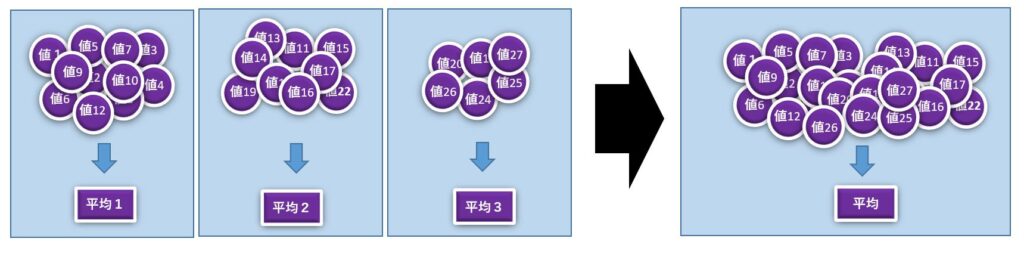
そもそも加重平均は、集団ごとに計算された平均値を、集団の規模を加味して平均するものですから、元の集団を1つに纏めてしまえば、集団の規模を加味する必要が無い訳です。
平均値は値の合計を個数で割ったものですから、逆に平均値と個数を掛けることで、値の合計が計算できます。
つまり、個々の集団ごとに平均×個数で合計を計算し、それらを全て足し合わせた後で、全ての集団の個数の合計で割ってあげるだけで良いのです。

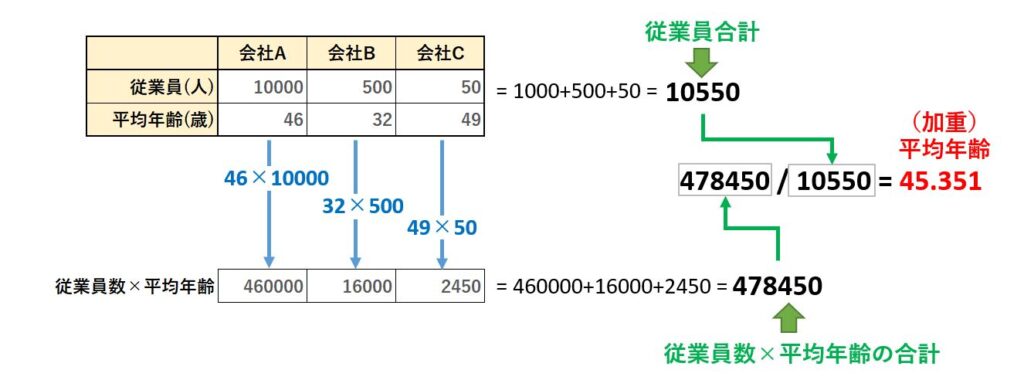
この考え方を使って、会社A~会社Cの加重平均を計算すると次の様になります。
方法1と方法2では、考え方が少し違いますが、結果は同じになります。
計算式で考えると、単純に分母の個数で先に割るか、後で割るかの違いにしかなりませんので、どちらかやりやすい方で計算して下さい。
まとめ
今回は加重平均についての求め方についての記事でした。
加重平均は、複数の平均値に対して、その平均値が計算された元の集団の規模を平均値に反映させる方法です。
複数の平均値から1つの平均値を求める場合、通常の平均を使うこともよく行われていますが、より厳密に計算したい場合には加重平均を使います。
今回の記事が皆様のお役に立てれば幸いです。


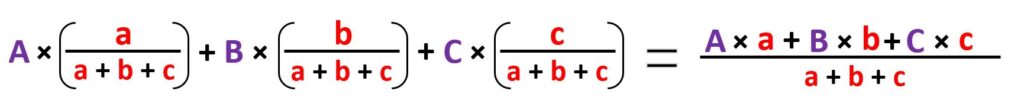
コメント